Development of a fast 3D MRI simulator using general-purpose graphic processor units

Several MRI simulators have been reported using various systems (1-4). Cost-performance is essential to MRI simulator, because MRI simulation suits parallel computing and the performance of the parallel computers is nearly proportional to their cost. In this study, we developed several simulation programs optimized for three general-purpose graphic processor units (GPGPUs), compared their speeds, and evaluated the validity using MRI experiments.
We used three GPGPUs (Tesla K80, GTX TITAN-Z, GTX 980, NVIDIA). GPGPU programs for Bloch-equation based MRI simulation were developed using the CUDA platform. MRI experiments were performed using a digital MRI system with a 9.4T/54mm superconducting magnet (5). Several 3D gradient-echo images of a phantom were acquired to evaluate the validity of the simulation.
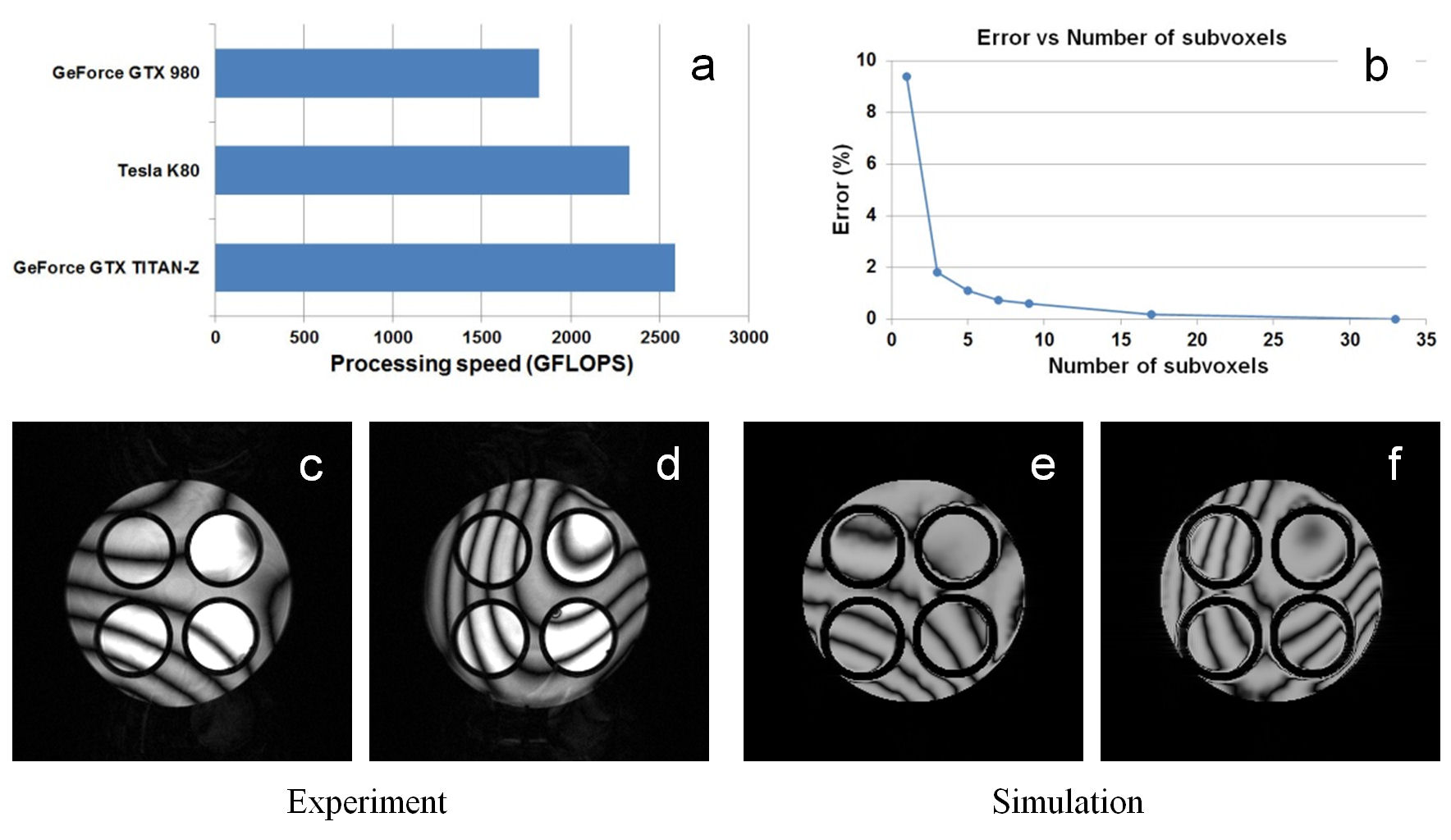
Figure 1a shows processing speed of a simulation program developed for a 3D TrueFISP sequence (number of voxels: 128³, number of subvoxels: 7) including the effect of the magnetic field inhomogeneity and relaxation times. The processing time for the fastest GPU was 95.2 s (about 6000 s for a 256³ matrix image). The calculation was performed using single-precision FP numbers and their theoretical processing speeds vary from 8.0, 5.6, and 4.6 to 10.0, 8.7, and 5.0 TFLOPS for TITAN-Z, K80, and GTX 980, respectively, because the speeds depend on their working temperature. Therefore, Fig.1a shows that the processing speeds were about 1/3 of the theoretical limits, which shows that the program was fairly optimized. Fig.1b shows computation error plotted against the number of subvoxels equally spaced along the readout direction. This graph shows that the number of the subvoxels is essential to the computation error, because the angles between RF pulses and nuclear magnetizations depend on the field inhomogeneity. Figs. 1c and d show 2D cross-sections of the phantom acquired with a TrueFISP sequence (TR=20ms, TE=10ms, matrix = 256x256x64) and Figs. 1e and 1f show correspondent cross-sections calculated using our MRI simulator. The calculation was performed using a numerical phantom and the measured field inhomogeneity. The good agreement between them demonstrates the validity of the MRI simulation. In conclusion, single-precision calculation is sufficient for MRI simulation and much faster system can be economically built using PC clusters equipped with GPGPUs.
Ref: 1.H.Benoit-Cattina et al. JMR 173,97(2005). 2.T.Stöcker et al. MRM 64,186(2010). 3.K.G.Baum et al. IJBI,1(2011). 4.C.G.Xanthis et al. IEEE MI 33:607(2014). 5.S.Hashimoto et al. MRMS13,285 (2014).