Quantificational Multi-dimensional NMR with T1, T2, D or Gint

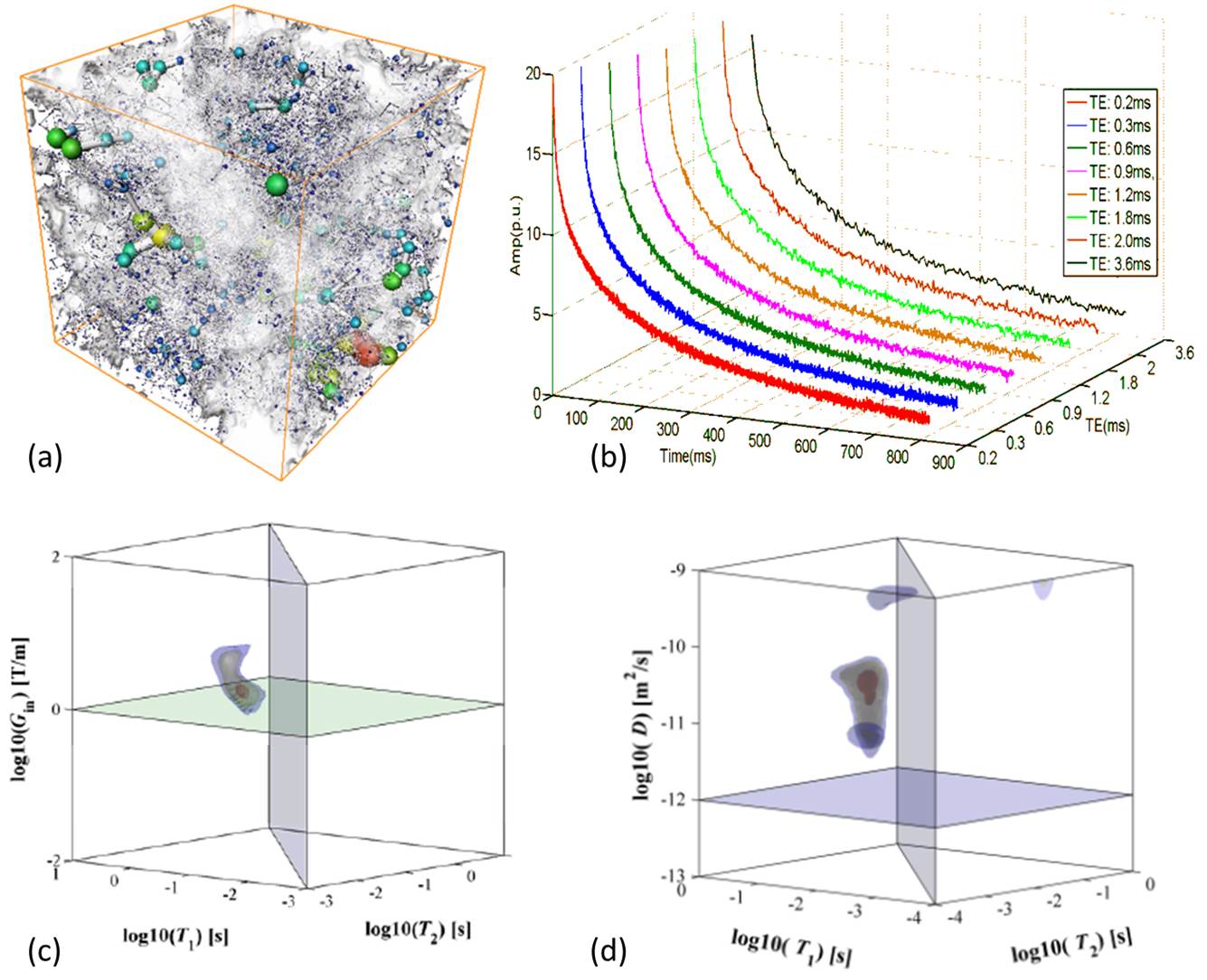
With the contrast between the molecule diffusion coefficients and relaxation time of fluids (oil and water), multidimensional NMR method has been considered to be a powerful tool to identify oil and water phases saturated in porous media (rocks) [1] [2] . Multidimensional NMR method is difficult to calculate the fluid properties quantificationally because of the restricted diffusion of fluid molecules and the internal magnetic field gradients caused by the differences of susceptibility between fluid and solid matrix in rock samples. X-ray CT with high resolution is employed to build a forward model for numerical simulation to study the interface effect between the solid phase and liquid phase. Magnetization transfer occurred between hydrogen nuclear in bound state and movable state is estimated quantificationally. The fast T1-DG2-T2 3D pulse sequence and Laplace inversion algorithm [3] are employed, which will be proved with core analysis experiments, to build a quantitative evaluation model. The research is important for the development of new methods of quantitative formation evaluation with NMR logging.