Postersession - P-075
A fast analytical calculation method for eddy current induced by gradient fields
- 1. Chongqing University, Chongqing, China
- 2. Chongqing Normal University, Chongqing, China
Introduction:
Eddy currents are inevitable in magnetic resonance imaging (MRI) system, they are mainly induced by gradient fields. The fast switching of gradient pulse with steep rising and failing edges will create spatially distributed transient eddy currents in the surrounding conducting structures. In this paper, we implement an analytical method to calculate the eddy currents induced by gradient fields in traditional "C" shape MRI system. Through this method, we can grasp the regularities of eddy currents distribution clearly.
Method:

Fig.1 Gradient pulse
The excitation of gradient pulse is shown in Fig.1, we use Fourier series expansion to express the pulse. It can be expressed as:
I(t)=2Aτ/T+∑sin(0.5n ω0τ) ·sin(0.5nω0 τr)/(0.5nω0τ)·sin(0.5n ω0τr)/(0.5nω0 τr)·e-jn ω0(τ+ τr)/2e(jn ω0t)
So the gradient current can be regarded as a combination of many time-harmonic currents components, and the magnetic vector potential of each time-harmonic current can be expressed as:
∇2A-jω μ(γ+jω ε)A=-μJs
By calculating the equations we can obtain A and eddy current distributions of each individual time-harmonic current components. In our research, we chose the basic frequency component and the first ten harmonic components, and sum their results to obtain a final eddy current distribution in metallic materials.
Results:
Fig.2 demonstrates the eddy currents on the metal surface which induced by z-gradient coil and x-gradient coil at t = 0.5 τr , respectively. From these figures, we can see the distribution of eddy currents clearly.
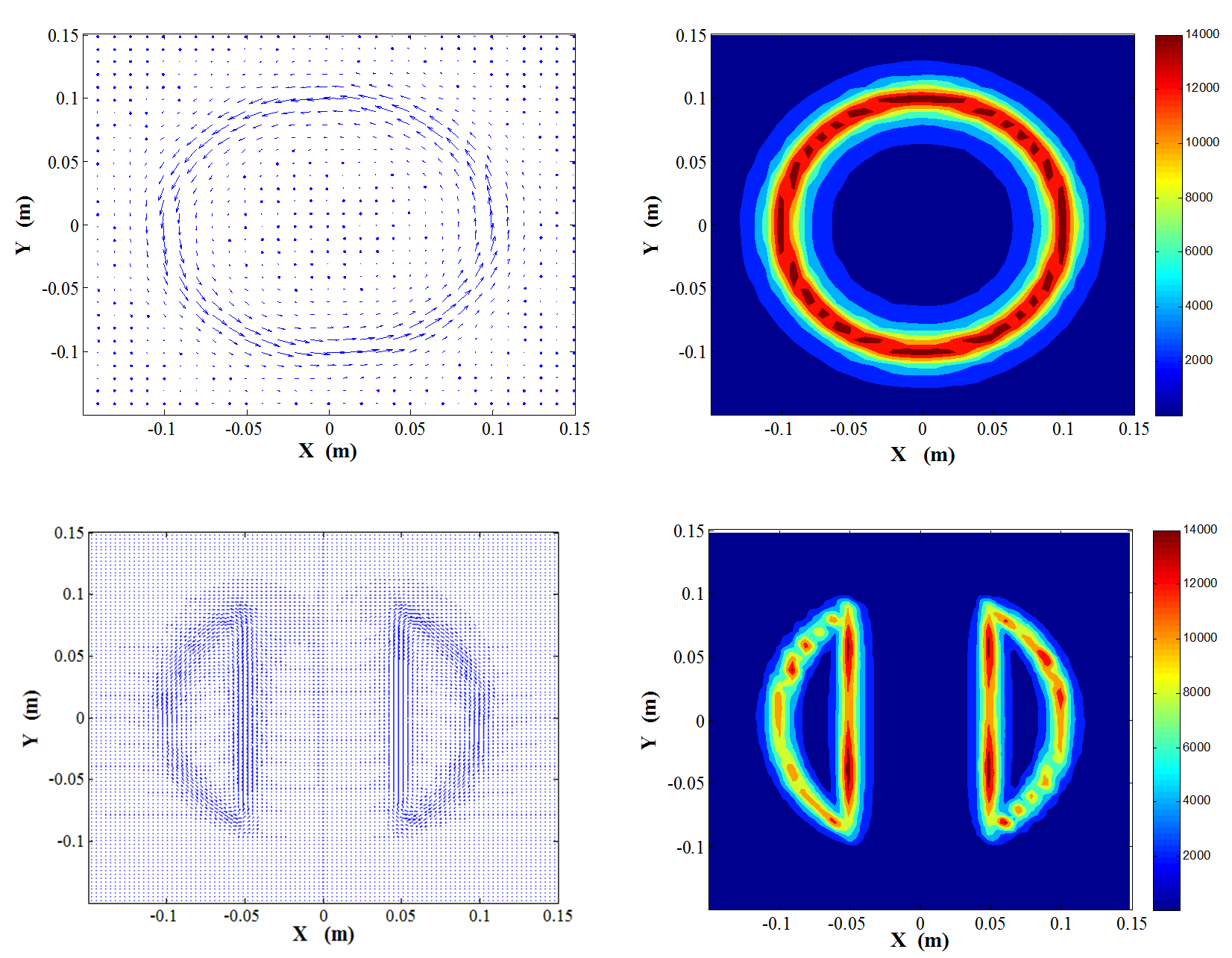
Fig.2 Eddy current induced by z and x gradient coil
Conclusion:
A fast analytical calculation method for eddy current induced by gradient fields was introduced. Comparing with the numerical method, this method is very fast and has a high calculation accuracy. This method can be used to simulate the transient process of gradient field with surrounding metallic materials.
