3D Motion of Magnetic Particles in Rotational Drift Spectroscopy

Introduction:
Rotational drift spectroscopy (RDS) is a new modality for the detection of magnetic nanoparticles in liquid suspension [1]. It inductively measures the nonlinear rotational behavior of magnetic particle ensembles in rotating magnetic fields. As this motion strongly depends on parameters of particles and environment, it offers potential for sensitive detection thereof. Understanding the time evolution of the magnetization vector of individual particles is fundamental for RDS and has been considered in more detail in this work.

Methods:
The motion of a magnetic particle in viscous solution is given by dm/dt = ζ^-1 m × B × m [4]. Here, m is the particle's magnetic moment and ζ its drag coefficient. For the simulation, a rotating magnetic field in the xy-plane with constant angular velocity ω₀ and amplitude B was applied and a rotating frame of reference with B aligned with the x-axis was chosen.

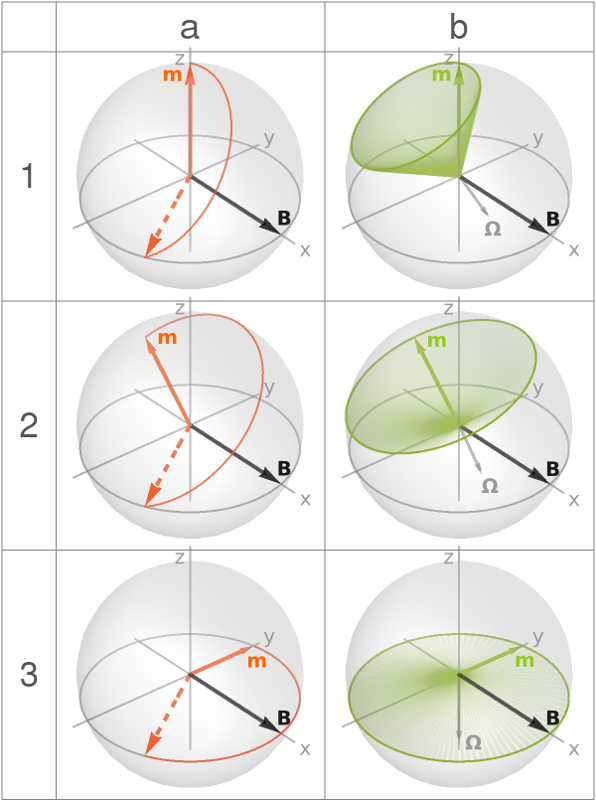
The analytical solution for the 2D motion of m in the xy-plane shows two different types of rotational behavior [2]: For driving frequencies ω₀ below or equal to a critical frequency Ω_c = ζ^-1 m B, m lags behind B with a locked phase difference. For ω₀ > Ω_c m exhibits a non-linear rotational drift with an increasing phase lag at periodically oscillating angular velocity Ω(t). Both the phase difference and the average angular velocity <Ω> only depend on the observed system and the external field - comparable to the Larmor frequency in magnetic resonance.

Since the 2D case is not sufficient for RDS, a numerical simulation using a semi-analytical Euler forward algorithm was implemented for a full 3D description of the time evolution of the magnetization vector and tested against the analytical solution for a motion restricted to the xy-plane.

Results & Conclusion:
As in 2D, the 3D motion shows two different types of rotational behavior depending on the ratio of Ω_c and ω₀. For ω₀ ≤ Ω_c the magnetization relaxes to the xy-plane resulting in the same time-constant phase lag as described for the 2D motion (fig.1a: Ω_c / ω₀ = 1.2). For ω₀ > Ω_c m performs a precessing motion around the orientation of the current vector of angular velocity Ω (fig. 1b: Ω_c / ω₀ = 0.6).

The simulations provide a better understanding of the underlying physical effects of RDS and serve as basis for further signal simulations covering particle systems, thermal noise and other field geometries.

Acknowledgement: This work is funded by the DFG (BE 5293/1-1).