NMR Diffusion Signal for Molecules Subject to Potentials

Translational diffusion of fluids can be observed by introducing magnetic field gradient waveforms into nuclear magnetic resonance (NMR) acquisitions. We studied the influence of diffusion on NMR experiments when the molecules undergo Brownian motion under the influence of a force field, and place special emphasis on parabolic (Hookean) potentials.

We tackled the problem theoretically using path integral methods and obtained explicit relationships for commonly employed gradient waveforms involving pulsed and oscillating gradients. The Bloch-Torrey equation, describing the temporal evolution of magnetization, is modified by incorporating the force field influencing the molecules' movements. A general solution to this equation is obtained for the case of parabolic potential by adopting the multiple correlation function (MCF) formalism, which has been used in the past to quantify the effects of restricted diffusion.

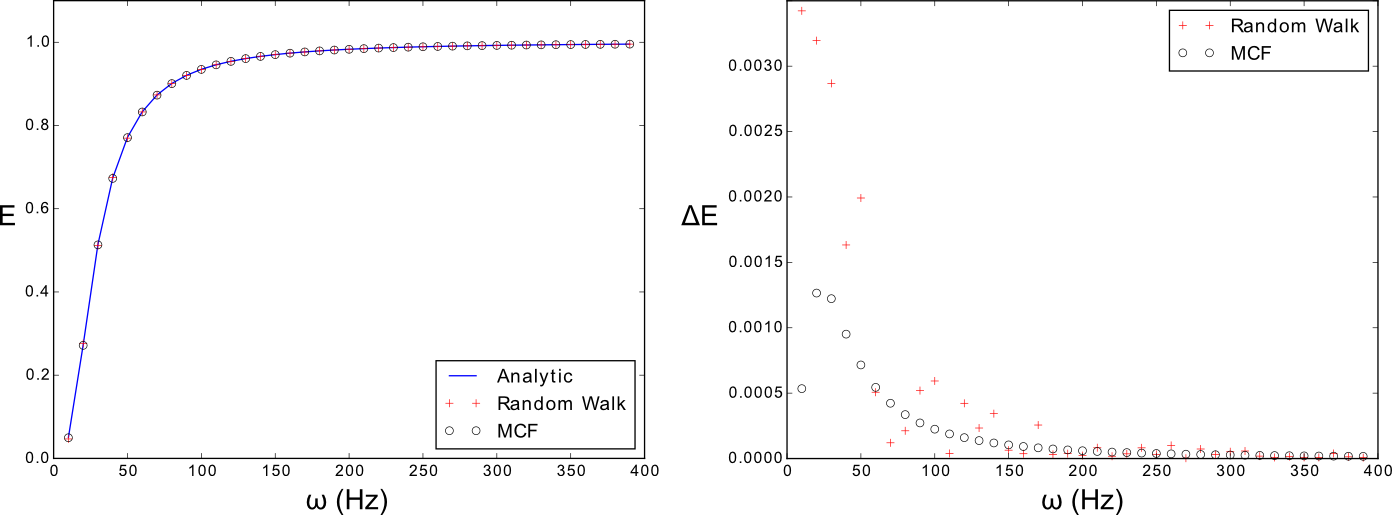
We also performed Monte-Carlo simulations to numerically validate the results obtained by the analytical (path-integral) and semi-analytical (MCF) methods described above. Figure 1 illustrates the agreement of these three methods.

Finally, we introduce a multi-dimensional formulation of the problem and achieve a new characterization of diffusional anisotropy. Unlike for the case of traditional methods that employ a diffusion tensor, anisotropy originates from the tensorial stiffness, and bulk diffusivity is retained in the formulation. This approach thus yields a viable alternative to diffusion tensor imaging [1] though features a different diffusion-time dependence, which is more suitable for realistic problems.

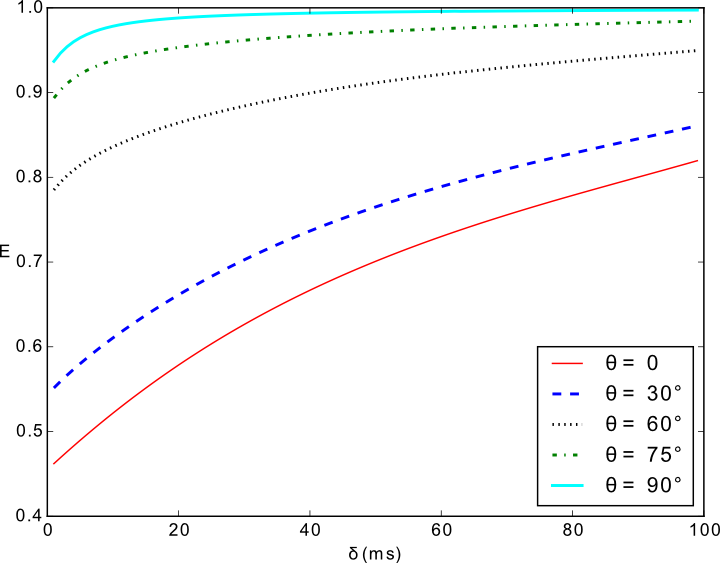
Our findings suggest that some features of the NMR signal that have traditionally been attributed to restricted diffusion are accommodated by the Hookean model. Under certain conditions, the formalism can be envisioned to provide a viable approximation to the mathematically more challenging restricted diffusion problems.